4.1 The best-fit line

Let me first start with an illustration. Say, we want to understand the relationship between education and income. Let’s first simulate the data and plot the relationship.

n  <- 1000
educ  <- sample(seq(1, 16, 1), n, replace = TRUE)
income  <- 20000 + 2000 * educ + rnorm(n, mean = 10000, sd = 5000)

dat  <- data.frame(educ = educ, income = income)

# mean income for each value of education
dat_sum  <- dat  %>% 
                group_by(educ)  %>% 
                summarize(mean_income = mean(income))

# merge 
dat  <- dat  %>% 
            merge(dat_sum, by = "educ", all.x = T)

f0  <- ggplot(dat, aes(x = educ, y = income)) + geom_point() + 
            geom_line(aes(x = educ, y = mean_income), size = 1) +
        xlab("years of education") + ggtitle("Panel A") + 
        annotate("text", x = 10, y = 35000, 
                label = "Line plotting the conditional mean", color = "blue", hjust = 0)

f1  <- ggplot(dat, aes(x = educ, y = income)) + geom_point() + 
geom_smooth(method = "lm", se = FALSE, color  = "blue") + xlab("years of education") + 
annotate("text", x = 10, y = 35000, label = "Best-Fit Line; E(Y|X)", color = "blue", hjust = 0) + 
ggtitle("Panel B")

f0 / f1

## `geom_smooth()` using formula = 'y ~ x'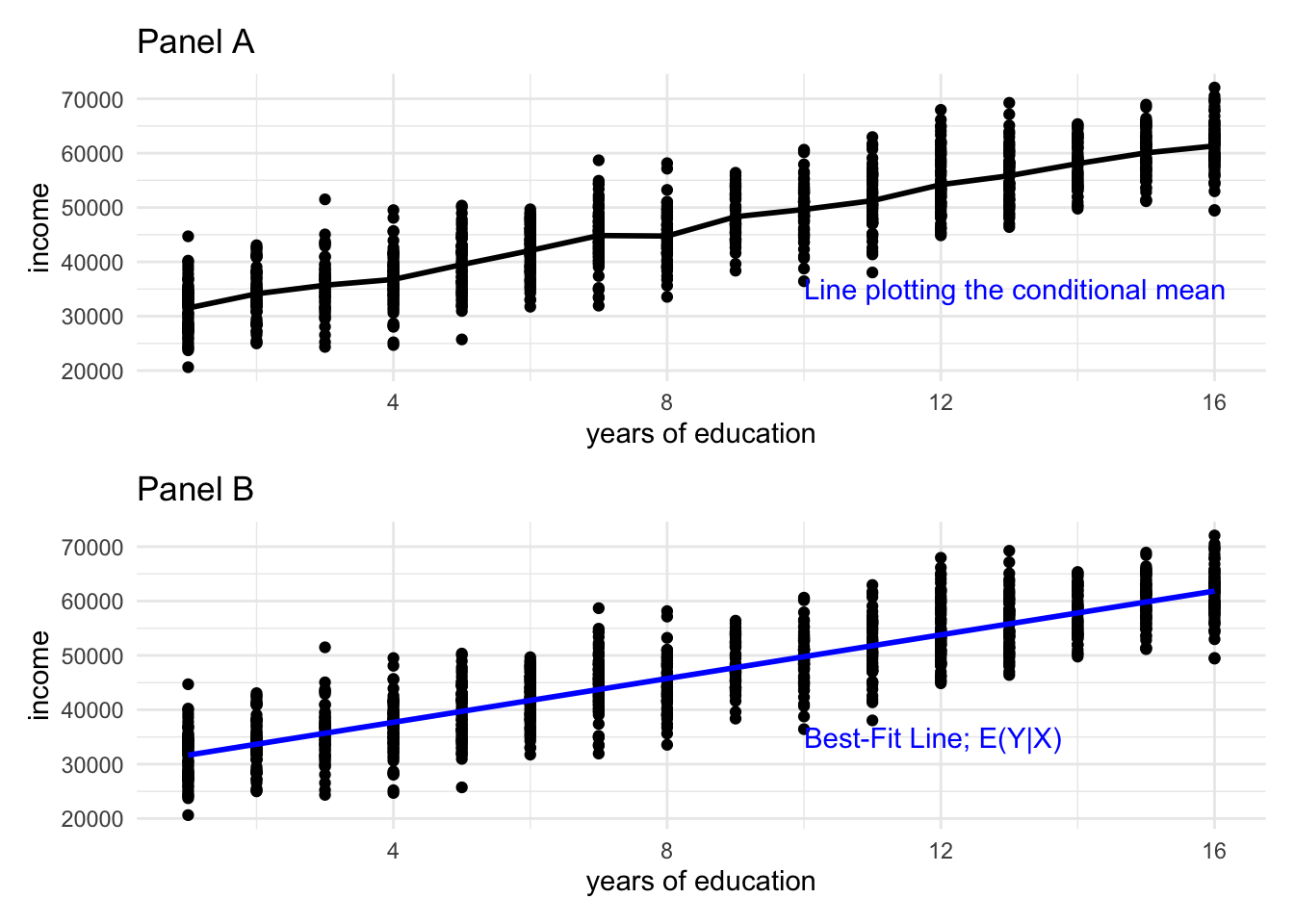

Each point on the figure pertains to an individual. Panel A uses the raw points, while Panel B adds in the best-fit line. This is also known as the regression line.